BlueRing1017 b7720d9e22424408aca0a6ccc76240d1
| 분야 | 스크립트 |
|---|---|
| 게임버전 | 모든버전 |
스크립트를 짜다보면 어딘가를 바라보게 해야할 때가 있습니다.
저는 이 기능을 구현 하기 전까지 마인크래프트 기본 커맨드인 /tp 의 facing을 사용했고,
커맨드를 쓰면 다들 알다시피 콘솔이 매우 더러워집니다.
실제로 구글링을 많이 해봤지만, 스크립트는 location 변수의 yaw값과 pitch 값으로 시야를 조절할 뿐, facing은 없습니다.
(제가 모르는 걸 수도 있습니다 :D)
그래서 facing을 어떻게 하면 구현할 수 있을까를 생각해 보았고, 꽤나 흡족한 결과가 나왔습니다.
일단 이 기능을 구현하기 위해서는 삼각함수를 알아야 하는데 간단히만 짚고 넘어가도록 하죠.
(저는 이거 하려고 수학 공부했습니다. 최대한 쉽게 설명하도록 하죠.)
일단 삼각함수중 tan(탄젠트) 라는 친구가 있습니다. 이 친구가 뭐냐?
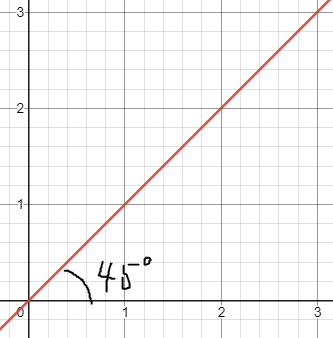
위의 그림처럼 특정 각도를 넣게되면
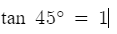
이렇게 기울기를 출력합니다.
(기울기는 다들 아시겠죠?)
하지만 여기서 문제가 있습니다.
마인크래프트 내에서 yaw 값은 360도, pitch 값은 180도, 즉 각도가 필요하지, 기울기가 필요하진 않습니다.
또한 기울기는 내 좌표와 바라볼 좌표로 충분히 구할 수 있죠
yaw 의 기울기 : (좌표1의 x좌표 - 좌표 2의 x좌표) / (좌표1의 z좌표 - 좌표 2의 z좌표)
pitch 의 기울기 : (좌표 1과 좌표 2의 x,z축 평면 상의 거리) / (좌표 1의 y좌표 - 좌표 2의 y좌표)
따라서 우리는 반대로 기울기를 넣으면 각도를 주는, 역함수가 필요합니다.
마침 탄젠트의 역함수 arctan(아크탄젠트) 가 있네요.
또한, 스크립트에서는 이를 함수화 해서 편하게 사용 가능합니다.
atan() 과 atan2() 가 바로 그 주인공인데요.
atan() 은 말 그대로 기울기를 넣으면 각도를 출력해주는 함수 입니다.
atan2() 는 평면상 좌표 1을 (0,0) 이라고 가정하고, 좌표 2의 값을 넣으면, x축과 좌표 1, 좌표 2를 이은 직선간의 각도를 출력합니다.
atan2() 가 더 사용하기 쉬워보이니, 저는 atan2()를 사용했습니다.
코드를 먼저 볼까요?
function facing2(e: entity, l: location):
set {_loc} to location of {_e}
set {_x} to x location of {_l} - x location of {_loc}
set {_y} to y location of {_l} - y location of {_loc}
set {_z} to z location of {_l} - z location of {_loc}
set {_yaw.tan} to atan2({_x}, {_z})
set yaw of {_loc} to {_yaw.tan} - 90
set {_pit.dis} to ({_x} ^ 2 + {_z} ^ 2) ^ (1 / 2)
set {_pit.tan} to atan2({_pit.dis}, {_y})
set pitch of {_loc} to {_pit.tan} * -1
teleport {_e} at {_loc}
위의 설명을 잘 읽으셨다면 이 코드를 이해하실거라 생각합니다.
(yaw 와 pitch 값에서 -90 과 * -1 은 시행착오를 거치면서 나온 결과입니다. 정확한 이유는 아직 모릅니다. 수학 싫어요)
그럼 잘 작동하는지 보죠.
/facing2 라는 명령어를 만들어, 주변의 에메랄드 블럭을 바라보게 만들었습니다.
잘 작동 하네요!
다만, 에메랄드의 위를 바라본다는것인데, 이것의 이유는

해당 사진처럼 엔티티의 좌표는 발바닥, 땅에 닿아있는 곳의 기준이기 때문에, 실제 시야가 있는 머리의 위치와 약 1.6칸 차이가 납니다.
이 차이가, 영상에서 나온것 처럼 약간 위를 바라보게 만드는 것이죠.
이것도 고치라면 고칠 수는 있겠는데, 너무 복잡해져서 다음에 기회가 되면 해보도록 하겠습니다.
생각보다 알아두면 매우 유용한 함수(무려 깨끗한 콘솔창)니, 잘 사용해보시기 바랍니다.









세티스
2021.08.04블럭 좌표라 그런거같은데 테스트 해보니깐 {_l}의 y좌표에 -1.5정도 더해주면 딱 맞네요.
BlueRing1017
2021.08.06그렇게 보니 생각보다 간단한 문제였군요! 감사합니다 :)
명이
2021.08.09이런글은 추천으로...
BlueRing1017
2021.08.10XD
미초는미초
2021.08.11흥미롭네요 블링씨^^
BlueRing1017
2021.08.28^^7
허두
2021.09.26한마탐 기출문제 (메모메모)
BlueRing1017
2021.09.27ㄷㄷ..